7 خوارزميات يجب أن يعرفها كل مبرمج

كطالب في البرمجة ، من المحتمل أنك تعلمت الكثير من الخوارزميات المختلفة طوال مسيرتك المهنية. إتقان الخوارزميات المختلفة أمر ضروري للغاية لأي مبرمج.

مع وجود العديد من الخوارزميات ، قد يكون من الصعب تتبع ما هو ضروري. إذا كنت تستعد لمقابلة أو ببساطة صقل مهاراتك ، فهذه القائمة ستجعل الأمر سهلًا نسبيًا. تابع القراءة حيث نقوم بإدراج أهم الخوارزميات للمبرمجين.

1. خوارزمية ديكسترا

كان Edsger Dijkstra أحد أكثر علماء الكمبيوتر تأثيرًا في عصره ، وقد ساهم في ذلك العديد من المجالات المختلفة لعلوم الحوسبة ، بما في ذلك أنظمة التشغيل وبناء المترجم والكثير أكثر. إحدى أبرز مساهمات Dijkstra هي براعة خوارزمية أقصر مسار للرسوم البيانية ، والمعروفة أيضًا باسم خوارزمية Dijkstra's Shortest Path.

تعثر خوارزمية Dijkstra على أقصر مسار منفرد في الرسم البياني من المصدر إلى جميع رؤوس الرسم البياني. في كل تكرار للخوارزمية ، تتم إضافة رأس بأدنى مسافة من المصدر ورأس غير موجود في أقصر مسار حالي. هذه هي الخاصية الجشعة التي تستخدمها خوارزمية دجيكسترا.

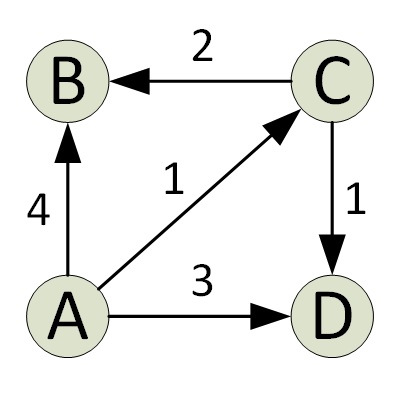
عادة ما يتم تنفيذ الخوارزمية باستخدام مجموعة. تعد خوارزمية Dijkstra فعالة للغاية عند تنفيذها باستخدام Min Heap ؛ يمكنك العثور على أقصر مسار في وقت O (V + ElogV) فقط (V هو عدد الرؤوس و E هو عدد الحواف في رسم بياني معين).

خوارزمية ديكسترا لها حدودها. إنه يعمل فقط على الرسوم البيانية الموجهة وغير الموجهة ذات الحواف ذات الوزن الإيجابي. بالنسبة للأوزان السالبة ، يفضل استخدام خوارزمية بيلمان-فورد.

تتضمن أسئلة المقابلة عادةً خوارزمية Djikstra ، لذلك نوصي بشدة بفهم تفاصيلها المعقدة وتطبيقاتها.

2. دمج الفرز

لدينا نوعان من خوارزميات الفرز في هذه القائمة ، ودمج الفرز هو أحد أهم الخوارزميات. إنها خوارزمية فرز فعالة تعتمد على تقنية البرمجة Divide and Conquer. في أسوأ السيناريوهات ، يمكن لفرز الدمج فرز الأرقام "n" في وقت O (nlogn) فقط. مقارنة بتقنيات الفرز البدائية مثل فقاعة الفرز (يستغرق ذلك الوقت O (n ^ 2)) ، دمج الفرز فعال بشكل ممتاز.

متعلق ب: مقدمة في دمج الفرز الخوارزمية

في فرز الدمج ، يتم تقسيم المصفوفة المراد فرزها بشكل متكرر إلى مصفوفات فرعية حتى يتكون كل صفيف فرعي من رقم واحد. تقوم الخوارزمية العودية بعد ذلك بدمج المصفوفات الفرعية وفرز المصفوفة بشكل متكرر.

3. الترتيب السريع

Quicksort هي خوارزمية فرز أخرى تعتمد على تقنية البرمجة Divide and Conquer. في هذه الخوارزمية ، يتم اختيار عنصر أولاً كمحور ، ثم يتم تقسيم المصفوفة بأكملها حول هذا المحور.

كما خمنت على الأرجح ، يعتبر المحور الجيد أمرًا حاسمًا لفرز فعال. يمكن أن يكون المحور إما عنصرًا عشوائيًا أو عنصر الوسائط أو العنصر الأول أو حتى العنصر الأخير.

غالبًا ما تختلف تطبيقات الترتيب السريع في طريقة اختيار المحور. في الحالة المتوسطة ، سيقوم الترتيب السريع بفرز مصفوفة كبيرة ذات محور جيد في وقت O (nlogn) فقط.

يقسم الكود الكاذب العام للفرز السريع المصفوفة بشكل متكرر على المحور ويضعها في الموضع الصحيح للمصفوفة الفرعية. كما أنه يضع العناصر أصغر من المحور على يساره والعناصر أكبر من المحور على يمينه.

4. عمق البحث الأول

يعد Depth First Search (DFS) أحد خوارزميات الرسم البياني الأولى التي يتم تدريسها للطلاب. DFS هي خوارزمية فعالة تستخدم لاجتياز الرسم البياني أو البحث عنه. يمكن أيضًا تعديله لاستخدامه في اجتياز الأشجار.

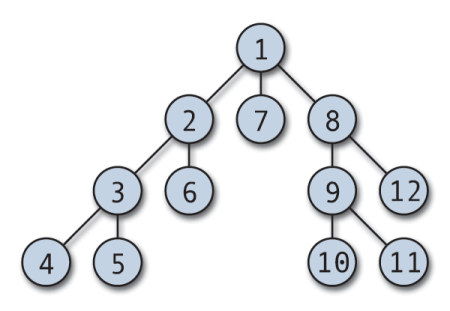
يمكن أن يبدأ اجتياز DFS من أي عقدة عشوائية ، ويغوص في كل قمة مجاورة. تتراجع الخوارزمية عندما لا يكون هناك قمة غير مرغوب فيها ، أو عندما يكون هناك طريق مسدود. يتم تنفيذ DFS عادةً باستخدام مكدس ومصفوفة منطقية لتتبع العقد التي تمت زيارتها. DFS سهل التنفيذ وفعال بشكل استثنائي ؛ إنه يعمل (V + E) ، حيث V هو عدد الرؤوس و E هو عدد الأضلاع.

تشمل التطبيقات النموذجية لاجتياز DFS الفرز الطوبولوجي ، واكتشاف الدورات في الرسم البياني ، وتحديد المسار ، والعثور على المكونات المتصلة بقوة.

5. اتساع البحث الأول

يُعرف البحث عن النطاق الأول (BFS) أيضًا باسم اجتياز ترتيب المستوى للأشجار. يعمل BFS في O (V + E) على غرار خوارزمية DFS. ومع ذلك ، يستخدم BFS قائمة انتظار بدلاً من المكدس. يتعمق DFS في الرسم البياني ، بينما يتجاوز BFS الرسم البياني في اتجاه عرضي.

تستخدم خوارزمية BFS قائمة انتظار لتتبع القمم. تتم زيارة القمم المجاورة التي لم تتم رؤيتها وتمييزها ووضعها في قائمة الانتظار. إذا لم يكن للرأس أي رأس مجاور ، فسيتم إزالة قمة من قائمة الانتظار واستكشافها.

يستخدم BFS بشكل شائع في شبكات نظير إلى نظير ، وهو أقصر مسار للرسم البياني غير الموزون ، وللعثور على الحد الأدنى من الشجرة الممتدة.

6. بحث ثنائي

بحث ثنائي هي خوارزمية بسيطة للعثور على العنصر المطلوب في مصفوفة مرتبة. إنه يعمل عن طريق تقسيم المصفوفة بشكل متكرر إلى النصف. إذا كان العنصر المطلوب أصغر من العنصر الوسيط ، فسيتم معالجة الجانب الأيسر من العنصر الأوسط بشكل أكبر ؛ خلاف ذلك ، يتم تقسيم الجانب الأيمن إلى النصف ويتم البحث عنه مرة أخرى. تتكرر العملية حتى يتم العثور على العنصر المطلوب.

إن التعقيد الزمني الأسوأ للبحث الثنائي هو O (logn) مما يجعله فعالاً للغاية في البحث عن المصفوفات الخطية.

7. الحد الأدنى من خوارزميات شجرة الامتداد

الحد الأدنى للشجرة الممتدة (MST) للرسم البياني لها أدنى تكلفة بين جميع الأشجار الممتدة الممكنة. تعتمد تكلفة الشجرة الممتدة على وزن حوافها. من المهم ملاحظة أنه يمكن أن يكون هناك أكثر من الحد الأدنى للشجرة الممتدة. هناك نوعان من خوارزميات MST الرئيسية ، وهما Kruskal’s و Prim’s.

تقوم خوارزمية Kruskal بإنشاء MST عن طريق إضافة الحافة بأقل تكلفة لمجموعة متزايدة. تقوم الخوارزمية أولاً بفرز الحواف حسب وزنها ثم تضيف حوافًا إلى MST بدءًا من الحد الأدنى.

من المهم ملاحظة أن الخوارزمية لا تضيف حوافًا تشكل دورة. تُفضل خوارزمية Kruskal للرسوم البيانية المتفرقة.

تستخدم خوارزمية Prim’s أيضًا خاصية الجشع وهي مثالية للرسوم البيانية الكثيفة. الفكرة المركزية في Prim’s MST هي الحصول على مجموعتين متميزتين من الرؤوس ؛ مجموعة واحدة تحتوي على MST المتزايد ، في حين أن الأخرى تحتوي على رؤوس غير مستخدمة. في كل تكرار ، يتم تحديد الحد الأدنى لحافة الوزن التي ستربط المجموعتين.

يعد الحد الأدنى من خوارزميات الشجرة الممتدة ضرورية لتحليل المجموعات والتصنيف وشبكات البث.

المبرمج الكفء ماهر بالخوارزميات

يتعلم المبرمجون مهاراتهم ويطورونها باستمرار ، وهناك بعض الأساسيات الأساسية التي يحتاج كل فرد إلى إتقانها. يعرف المبرمج الماهر الخوارزميات المختلفة ، ومزايا وعيوب كل منها ، وأي خوارزمية ستكون الأنسب لسيناريو معين.

مقدمة في خوارزمية فرز شل

في حين أن فرز الصدفة ليس الطريقة الأكثر فاعلية ، فإن المبتدئين لديهم الكثير للاستفادة من ممارسته.

اقرأ التالي

نبذة عن الكاتب